It is easy to criticize journal metrics, especially when they do not provide the desired output. Authors and editors often espouse the metric that makes them look the best. And the loudest voices against journal metrics often come from those who are poorly ranked. When it comes to metrics, the ends often justify the means.
In the construction of journal metrics, there is no rule that indicators must be simple or treat their data fairly.
The Eigenfactor and SCImago Journal Rank (SJR), for example, are calculated using complex, computationally laden processes that give higher weight to citations from highly cited journals. Similarly, the Source-Normalized Impact per Paper (SNIP) attempts to balance the great inequality in the literature by giving more influence to citations in smaller disciplines with less frequent citation rates. Viewed in contrast, the impact factor is much more simple and egalitarian in its approach by giving equal weight to all indexed citations. Each of these approaches to create a simple metric are correct (if they report what they say they are counting), yet are based on different underlying values and assumptions.
In October 2011, the F1000 announced a new metric for ranking the performance of journals based on the evaluations of individual articles. As a direct challenge to Thomson Reuters, many are interested to see just how F1000 journal scores would stack up against the industry standard impact factor — a topic featured in this month’s issue of Research Trends.
I am less concerned with the performance of individual journals than I am in understanding the thought that went into the F1000 Journal Factor, what it measures, and how it provides with an alternate view of the journal landscape. When I wrote my initial review of the F1000 Journal Factor, I expressed three main concerns:
- That the F1000 Journal Factors were derived by a small dataset of article reviews contributed by a very small set of reviewers.
- That the F1000 gave disproportionate influence to articles that received just one review. This made the system highly sensitive to enthusiastic reviewers who rate a lot of articles in small journals.
- That the logarithmic transformation of these review scores obscured the true distance in journal rankings.
To underscore these points, I highlighted what can happen when the Editor-in-Chief of a small, specialist journal submits many reviews for his own journal. In this post, I will go beyond anecdotal evidence and explore the F1000 from a broader perspective. The following analysis includes nearly 800 journals that were given a provisional 2010 F1000 Journal Factor (FJF).
Predicting a Journal’s F1000
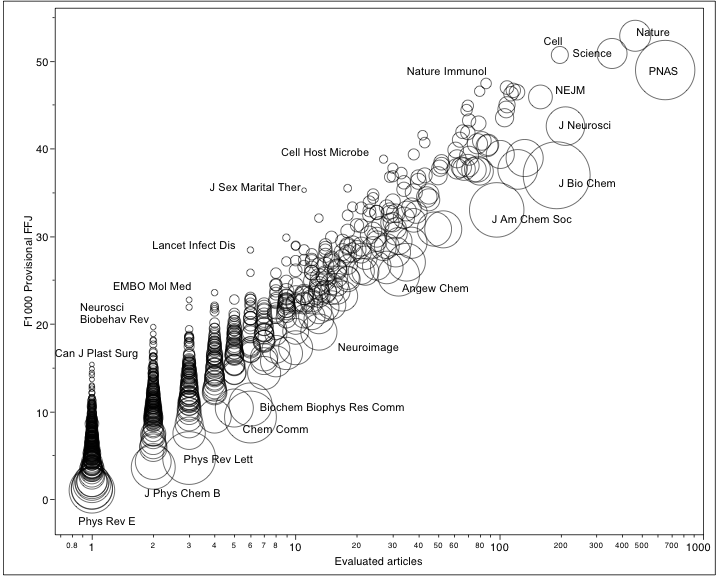
The strongest predictor of a journal’s F1000 score is simply the number of article evaluated by F1000 faculty reviewers, irrespective of their scores. The number of article evaluations can explain more than 91% of the variation in FJFs (R2=0.91; R=0.96). In contrast, the impact factor of the journal can only explain 32% of FJF variation (R2=0.32; R=0.57).
The rankings of journals based on F1000 scores also reveals a strong bias against larger journals, as well as a bias against journals that have marginal disciplinary overlap with the biosciences. The following plot reveals these biases.
Larger journals, represented by bigger circles in the figure above, consistently rank lower than smaller journals receiving the same number of article evaluations. This pattern is most apparent in the lower left quadrant of the graph where journals received 10 or fewer article reviews. In addition, as the FJF is calculated based on the proportion of submitted reviews compared to the number of eligible articles, journals in the physical sciences consistently rank lower than biomedical journals.
To underscore this point, the Canadian Journal of Plastic Surgery and Physical Reviews E — Statistical, Nonlinear and Soft Matter Physics, both received just one review in 2010. The former published just 24 eligible articles while the latter published 2,311. As a result, Can J Plast Surg was given a FJF of 15.36 while Phy Rev-E received a FJF of just 1 — the lowest possible score in F1000. The disparate FJF scores between these two journals is a function not of the quality of the articles they publish but of their size and subject discipline.
Other large physical science journals performed just as miserably under this calculation, while small biomedical journals performed exceptionally well.
At the other end of the graph, the bias against large journals and physical sciences journals seems to attenuate, with journals like Nature, Science, Cell, NEJM, and PNAS occupying the highest-rank positions. Unfortunately, journals occupying this quadrant don’t seem to tell us anything that we don’t already know, which is, if you want to read high-quality articles, you find them in prestigious journals. In this sense, post-publication peer review doesn’t offer any new information that isn’t provided through pre-publication peer review.
In defense of systemic bias against the physical sciences, we should remember that F1000 focuses on biology and medicine and that we shouldn’t be surprised that a core journal in statistical, nonlinear and soft matter physics (Phys Rev E) ranks so poorly. On the other hand, there are many core chemistry journals, like J Am Chem Soc (JACS), which rank very highly in F1000 simply because disciplinary boundaries in science are fuzzy and overlap. The desire to reduce size, discipline, and individual article scores into a simple unidimensional metric obliterates the context of these variables, leaving users with a single metric that makes little sense for most journals.
Journal metrics are supposed to simplify a vast and complex data environment. Like impressionistic paintings constructed through the technique of pointillism, we should be able to stand back and see meaningful pictures formed from a field of dots, each of which contains very little meaning in isolation. The construction of the F1000 Journal Factor appears to do just the opposite, creating a confusing picture from a dataset of very meaningful dots.

Discussion
17 Thoughts on "Size and Discipline Bias in F1000 Journal Rankings"
Thanks Phil. This is an Interesting and useful analysis. As I am sure you know, its possible to game other indexes such as the JCR as pointed out by Douglas Arnold and Kristine Fowler in Nefarious Numbers in Notices of the AMS. http://www.ams.org/notices/201103/rtx110300434p.pdf.
David. This is not about gaming an index, but systemic bias that is built into the construction of the F1000 Journal Factor against large journals and those in the physical sciences.
Sorry, you are correct. I was responding to your first concern above and the discussion of Sex and Marital Therapy in your earlier article.
Thanks for this Phil- it’s a fascinating graph.
I still find it strange that F1000 would see an academic need for this metric. Their individual article evaluations are fine and dandy, but the evaluations are only ever on about 5% (I’m guessing?) of a journal’s output it’s hard to see why they would be informative about the journal as a whole.
Sarah Huggett did the math and reported in Research Trends that more than 85% of the journals evaluated had less than 5% of their papers evaluated. To quote:
Looking at the 2010 provisional journal rankings, only 5 titles had more than 50% of their papers evaluated, less than 8% of journals had more than 10% of their articles reviewed, and more than 85% had less than 5% of their papers evaluated.
Phil, I think I am missing the point of part of your analysis. You show that “larger journals (…) consistently rank lower than smaller journals receiving the same number of article evaluations.” Isn’t this exactly how it should be? What I understand from it, these evaluations serve as a kind of recommendations. From this perspective, they are comparable with citations. If we have a small and a large journal and both journals have the same number of citations, then we usually rank the larger journal below the smaller one (e.g., according to impact factor or some other journal measure). The rationale is that on an average basis per article the smaller journal has been cited more frequently. Your analysis shows that the F1000 journal measure is doing something similar, with citations replaced by peer recommendations. In my view, this suggests that the F1000 journal measure behaves as it should be.
Notice that I do think there are some problems with the F1000 journal measure, but I don’t think large journals have an unfair disadvantage. In fact, I think it may even be argued that there is a bias the other way around, that is, against smaller journals (see my comments in the Research Trends article).
Hi Ludo. I think your comparison to citation metrics is inaccurate. When journal A receives a citation from journal B, we know this is a valid observation. When journal A does not receive a citation from journal B, we also know this is a valid observation, given that both journals are fully indexed.
In comparison, when journal A receives an article recommendation from a F1000 reviewer, we know this is a valid observation, but we do not know the meaning of no article recommendation. The lack of a recommendation could mean two distinct things:
1. That the article was read but just not worthy of a recommendation, or
2. That the article was simply not read by a F1000 faculty member.
Given the limited number of F1000 reviewers and the low frequency that most reviewers contribute (on average), we are mostly dealing with the second case. However, we are still left with the ambiguity of what the lack of a review means. Put another way, we don’t know if the cell in matrix is zero (case 1) or empty (case 2). When constructing a citation index, where the journal set is defined and all citation events are indexed, a non-citation event is always a zero –never an empty cell.
Since there are journals indexed in F1000 but are outside the biomedical field and have no assigned F1000 faculty reviewers, it is not surprising to see how poorly the physical science journals do — even the prestigious physical science journals. Their poor scores don’t reflect poor quality articles published in these journals, but simply the fact that no F1000 faculty member evaluated them. In other words, the F1000 Journal Factor fundamentally confuses quality with scope.
Hi Phil, I agree with what you are writing (although I think citations may suffer from similar problems as the F1000 recommendations, albeit to a lesser extent). But I don’t see how the mechanism you are describing leads to a bias against larger journals.
Looking at the formulas underlying the calculation of the F1000 journal measure (see http://f1000.com/about/whatis/factors), my conclusion is that in the case of a larger journal and a smaller one that do equally well in terms of average recommendation per article, the larger journal has a higher F1000 journal measure than the smaller one.
Consider the following example. (For simplicity, I skip the logarithmic transformation at the end of the calculation of the F1000 journal measure.) Journal A has 100 publications, and 20 of these have a (single) recommendation. Journal B has 1000 publications, and 200 of these have a (single) recommendation. For simplicity, assume all recommendations are of the ‘exceptional’ type. For journal A, we obtain a score of (Sum of article factors) * (Normalization factor) = (20 * 10) * (20 / 100) = 200 * 0.2 = 40. For journal B, we obtain (200 * 10) * (200 / 1000) = 2000 * 0.2 = 400. So journals A and B have the same average performance per article, but yet journal B has a higher score than journal A, just because journal B is larger than journal A.
My conclusion from this is that, if there is a size bias in the F1000 journal measure, the bias is in favor of larger journals over smaller ones rather than the other way around.
Hi Ludo, your math is good and I accept the derivation of the theory, yet the Figure I produced from the actual data suggests just the opposite, that there is a strong bias in favor of small journals. What do you think could explain this phenomenon?
Hi Phil, in my view, the reason why your figure suggests a bias in favor of smaller journals has to do with in the way in which the figure is constructed. The underlying assumption of your figure seems to be that journals with the same total number of recommended articles should have similar FFj scores. From this perspective there is indeed a bias in favor of smaller journals.
My perspective is that journals with the same average number of recommended articles (i.e., the same proportion of recommended articles) should have similar FFj scores. In that case, FFj scores have a bias in favor of larger journals.
Mathematically, this can be seen as follows. FFj essentially equals
(Sum of article factors) * (Normalization factor) = (Sum of article factors) * (Recommended articles / Total articles)
To keep things simple, let’s assume there is just one type of recommendation (instead of three), and let’s assume articles never have more than one recommendation. In that case, the above formula is proportional to
(Recommended articles) * (Recommended articles / Total articles)
The underlying assumption of your figure seems to be that FFj should be (more or less) proportional to a journal’s total number of recommended articles. In that case, the second factor in the above formula causes a bias in favor of smaller journals (since for these journals the denominator in this factor has a low value, which causes the overall factor to have a high value).
From my perspective, FFj should be proportional to a journal’s average number of recommended articles, or in other words, to the ratio of Recommended articles and Total articles. In that case, the first factor in the above formula causes a bias, but this time the bias is in favor of larger journals (since in the case of two journals for which the second factor is the same, the larger journal will have a higher value for the first factor).
So it depends on the perspective one takes whether there is a bias, and if so, in which direction. One of the reasons why I prefer my ‘average perspective’ over your ‘total perspective’ is that the average perspective is in agreement with the perspective taken by most citation-based journal indicators. These indicators usually aim to measure the average impact of the articles in a journal, not the total impact. Because most researchers are familiar with journal impact indicators, especially the impact factor, I think they will more or less automatically assume that a new journal indicator such as FFj also takes the average perspective.
Hi Ludo. I agree that for a citation index, measuring average citations would be preferable over total citations. However, as described in my earlier reply, calculating the average score only makes sense if you have valid observations for all of the articles; otherwise, you are assuming that every one of your empty cells in your dataset is a zero. The effect of assuming all empty cells are zeros radically depresses the total impact score of a poorly-reviewed journal, which is why larger journals fare much more poorly in the rankings.
You can do this –either in Excel or as a thought experiment– by calculating the average for a set of numbers when missing observations are assumed to be zeros or left as empty cells.
F1000 could address this ambiguity by having their faculty reviewers enter articles that were read but not recommended and assigning them a value of zero. In that way, we could tell the difference between valid evaluations and non-observations. As it stands, calculating a journal-level metric with a dataset that is mostly full of non-observations (empty cells) and assuming they are valid observations (zeros) is a fundamental problem with their journal metric. Coming up with a different algorithm to normalize their scores will only further obscure the real problem that lays beneath.
Ludo,
With regard to whether the total number of evaluations or the percent of evaluations are an accurate measure of influence, consider the following figure where I plot and regress the percentage of article evaluations to the journals’ Thomson Reuters Impact Factor. I use the Impact Factor as an external measure of journal “quality.” I realize that the Impact Factor is not a perfect measure, but we need something against which to measure what is going on in the F1000 evaluations.

If we consider the entire dataset (768 journals), the relationship between Pct Evaluated and Impact Factor is not bad. The model can explain 43% of the variation (R2=0.43 or R=0.66).
Now let’s focus on journals that received F1000 evaluations on 5% or fewer of their articles. This subset comprises 629 journals (or 82% of the entire dataset). When we regress the same variables, our R2 drops from 0.43 down to 0.036. In other words, percent evaluated articles can explain less than 4% of the variation. If this were a casino, the odds of making a good prediction are about the same odds of winning at the roulette wheel.
What does this mean? For the vast majority of the journal data, the percentage of evaluated articles has little baring on measuring the quality of the journal. Or conversely, that the relationship between evaluated articles and the Impact Factor is driven almost exclusively by the high-profile journals where we have no doubt of their standing.
The solution to this variability problem is simply to drop journals that receive few faculty evaluations. Unfortunately, this step would eliminate the vast majority of journals in their product.
Hi Phil, on this point we don’t agree with each other. In my view, you would have a valid point if F1000 evaluations could be either negative or positive. Suppose three types of evaluations were possible: Poor research (score 0), average quality research (score 5), and excellent research (score 10). In that case, it would be incorrect to treat an article without any evaluations as a 0 score. It would mean that the absence of an evaluation implies that the article presents poor research. This would of course make no sense. But in the F1000 system evaluations are always positive (just like citations are always assumed to be ‘positive’ in citation-based journal indicators), and therefore I don’t see the problem.
You are suggesting to allow reviewers to indicate they have read an article but don’t want to recommend it. In a sense, your proposal means that a fourth type of evaluation is added: The evaluation ‘not recommended’ is added to the existing evaluations ‘recommended’, ‘must read’, and ‘exceptional’. I think your suggestion has some merit, but I don’t think it is a necessity to have this fourth type of evaluation. Again a comparison can be made with citation metrics. If an article has no citations (or only a few of them), this could be either because people haven’t read the article and therefore don’t know about it or because people did read it but didn’t like it. Citation metrics cannot distinguish between these two scenarios. Nevertheless, we consider it acceptable to calculate impact factors and other similar metrics.
Hi Ludo,
I think you for the constructive ongoing discussion. I disagree that the lack of citation to an article can be compared to the lack of a faculty recommendation to an article. You are correct that it is impossible to understand the meaning of a missing citation, however, there are some key differences between citation behavior and recommendation behavior:
First, it is possible to give negative citations where this is not possible to do in the F1000 system. Authors give negative citations all the time without ripping another study to shreds.
Second, there are checks in the review process to ensure that the important literature is not ignored. A good reviewer will spot when the author is not giving credit to the relevant literature or suggest other studies to read and cite. In the F1000 system, no one tells a faculty reviewer what they should review.
Last, a reviewer system is not comparable to a citation network because a) a reviewer system is based on a sample and not a census; and b) we cannot consider the F1000 reviewer system to be an unbiased sample. While F1000 attempts to balance the number of reviewers proportionately to the amount of literature generated, these reviewers cover less than 2% of the literature and, not surprisingly, most reviewers provide very few (if any) reviews. Such is a system built on voluntary labor from busy scientists.
Phil, I agree with most statements in your last two posts. The F1000 journal measure indeed seems to have a reliability problem due to the limited number of reviews on which it is based. This problem may be reduced in the future if either the number of reviewers in the system is increased or the existing reviewers become more active. The analogy between citation measures and peer review measures is indeed far from perfect, but in my view it is sufficiently strong for the point I wanted to make in my previous message.
Our discussion started with my criticism on your claim of a bias in the F1000 measure in favor of small journals. I believe your claim of such a bias is too strong, but I do agree with some of your other points of criticism on the F1000 measure. Especially the limited reliability of the measure is an important problem.
Dear Phil and others:
A couple of clarifications:
First: We didn’t launch the FFj as a challenge to Thomson Reuters’ Impact Factor. Each of the metrics Phil mentions in his article is informative in its own way, and we believe our Journal Factor (FFj), as a fundamentally different, opinion-based metric, can make a useful contribution – alongside all the others – to the science (or the art) of assessing journals.
Second: As Phil says near the end of his piece, F1000 does not systematically cover physical sciences journals. We cover biology and medicine. Articles in physical science journals will occasionally be selected by our Faculty Members when there is sufficient cross-over interest to justify their inclusion, but this doesn’t happen often. So of course Phys Rev E performs “miserably” in our journal rankings – we wouldn’t expect it to do well. Given our clear biology/medicine focus it’s surprising to see it listed at all.
We disagree with Phil’s contention that the FFj, as currently calculated, has a bias against larger journals. In fact, as Ludo Waltman pointed out in his contribution to Sarah Huggett’s Research Trends article, there is actually a bias in favor. Our intention is that should be no bias either way, so, prompted by Ludo’s comments and with his assistance, we are working on a revised algorithm that eliminates journal size variations from the picture.
Our Rankings are in beta release for a very good reason; we had a pretty good idea when we launched that there would be refinements to come and we’re grateful to Sarah and Ludo for their thoughtful critique – they have helped us to see how we can improve the FFj and make it more useful and informative.
Lastly, we agree that the F1000 Journal Factor (FFj) doesn’t say much that’s new about journals at the top level, though we’re damned if we do and damned if we don’t – if our rankings follow the same pattern as the Impact Factor everyone says the FFj is unnecessary, if they don’t everyone says it must be wrong. In any case, it’s at the section and subspecialty level that the numbers can be most interesting.
Jane Hunter